表面自由エネルギーとは
表面自由エネルギー(surface free energy)とは、固体における液体での表面張力に当たるもので、固体の表面自体がもつ分子のエネルギーのことをさします。通常、表面張力は、mN/mの単位で表されるのに対し、表面自由エネルギーは、単位面積あたりのエネルギーとしてmJ/m2と表示されます(単位は異なりますが値は等しくなります)。
濡れの現象は、固体と液体それぞれの表面張力、及び固体/液体間の界面張力のバランスによって決まります(Youngの式)。

一般的には、液体の表面張力が小さく、固体の表面張力が大きいほど、濡れも良くなると言われています。しかし、実際には、表面張力はほぼ同等でも濡れが異なる場合があります。
このような現象を説明するために、表面自由エネルギー(表面張力)の成分分けという概念が提唱されています。
固体の表面自由エネルギーの数値は、液体のそれにくらべ大きく、測定方法も接触角を利用したものが主流です。
表面張力と表面自由エネルギー
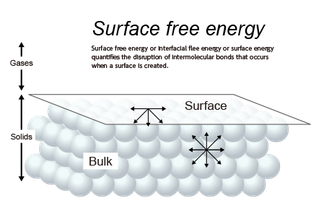
いま、大気と接している液体の様子を分子レベルで考えてみます。
バルク中のある1個の分子に着目すると、周辺分子との間には「分子間力」がはたらいています。このため、分子同士は互いに引き合っていますが、全体としては打ち消し合っており、バルクに存在する分子は比較的安定的です。
一方、表面(厳密に言えば、液体と気体との「界面」)に存在する分子に着目すると、バルク側の分子だけでなく、大気中の分子との間にも分子間力がはたらいています。
しかし、バルク側の分子の密度が圧倒的に高いため、表面に存在する分子は、常に内部に引き込まれています。この結果、表面を縮めるような張力がはたらいているように見えます。
これが「表面張力」です。
一方、エネルギー的には、バルク分子は、周辺分子と分子間力で引き合う、つまり、相互作用することによってエネルギーを下げています。しかし、表面分子は、大気側に相互作用の相手が少ないため、その分エネルギーが高くなっています。この表面分子がもつ過剰なエネルギーが「表面自由エネルギー」です。
表面張力は、単位長さにはたらく張力としてとらえられ、「力/長さ」の次元(単位は、例えばmN/m)を持ちますが、

のように表すことができるため、表面を単位面積だけ拡げるのに必要なエネルギー、または単位面積の表面に蓄えられるエネルギーと考えることができます。
すなわち、表面張力は「エネルギー/面積」の次元(単位は、例えばmJ/m2)をもつと考えることもでき、このように考えた表面張力は、「表面自由エネルギー」とよばれます。
このような考え方は固体表面(あるいは固体/液体界面、固体/気体界面、液体/液体界面)にも拡張することができます。
表面自由エネルギーの成分
以上のように、表面張力は分子間力に由来します。また、表面自由エネルギーと表面張力は等価です。一方、分子間力にはいくつもの種類があることから、表面自由エネルギー(または表面張力)についても、分子間力の種類に基づいて成分を分けるという概念が提唱されています。表面自由エネルギーの成分分けの概念で登場する分子間力は主として、配向力、誘起力、分散力、水素結合力です。
配向力、誘起力、分散力は、ファンデルワールス力(ファンデルワールスりょく、英: Van der Waals force)と総称されます。
配向力
双極子-双極子間の相互作用によって発生する力を言います。全体としては中性の分子が、電荷密度の偏りによって部分的に正負の電荷を帯びる場合があります(永久双極子)。
このような場合に、永久双極子をもつ分子同士が近接すると正負が向き合うように配向して発生する静電気力を言います。
誘起力
双極子-誘起双極子間の相互作用によって発生する力を言います。極性分子が無極性分子に近接すると、無極性分子に双極子を誘起し、その結果生じる静電気力のことです。
一般的に非常に小さいため、表面自由エネルギーの理論では通常無視されています。
分散力
無極性分子であっても、分子振動のために瞬間的に双極子が発生します。そうした際に無極性分子同士が近接したときに生じる相互作用によってはたらく力をいいます。
水素結合力
ある分子に水素原子が含まれている場合などに、電子の供与性が高い他の分子との間にはたらく力をいいます。ファンデルワールス力(Van der waals force)よりも強い力を持ちます。
Youngの式とDupréの式
いま、固体表面に1滴の液体を滴下し、この液体が固体をぬらしていく場合を考えます。
この液滴は、固体表面に接触した瞬間から固体表面でぬれ拡がり始めますが、あるところでぬれ拡がりが止まり、液滴が静止します。
端点では、固体の表面張力(気体/固体間の界面張力)、液体の表面張力(気体/液体間の界面張力)、液体/固体間の界面張力の3つの力がはたらいています。
表面張力(または界面張力)は、物質表面(または界面)の面積を小さくしようとする力ですので、端点にはたらく3つの力は、それぞれ、表面または界面の面積を小さくする方向にはたらきます。

これら3つの力のバランスによって、ぬれの状態、すなわち接触角θが決まります(いわゆるYoungの式)。
・・・・・・・・・・・・・・・・・・・・・・・(1)
一方、液体が固体をぬらしている時に、固体と液体をその界面で引き離す場合を考えます。 液体と固体との界面は、界面自由エネルギー を持ちます。この界面を引き離すのに必要なエネルギーは付着仕事(または接着仕事) とよばれます。
この界面に、外部から に相当するエネルギーを加えて引き離すと、新たな表面が生じます。
この新たな表面はそれぞれ , の表面自由エネルギーを持ちます。
このとき、引き離す前と引き離した後では、エネルギーの総和は等しいので、次のDupréの式が成り立ちます。
・・・・・・・・・・・・・・・・・・・・・・・(2)

(1)式と(2)式よりYoung-Dupréの式、
・・・・・・・・・・・・・・・・・・・・・・・(3)
が得られます。
いわゆる表面自由エネルギー解析理論とは、固体や液体の表面自由エネルギーをどのような成分に分けるか、そして上記の を、表面自由エネルギー成分を使ってどのように表現するかについての理論と言っても過言ではありません。
この の表し方については、いくつかの理論があります。表面自由エネルギー成分が既知の液体を用いて、表面自由エネルギーが未知の固体との接触角θを求めれば、それぞれの理論に基づいて固体の表面自由エネルギーを計算することができます。
表面自由エネルギーの理論式
表面自由エネルギーの理論式には、下記の方法が代表的です。
※ オプション『表面自由エネルギーライセンス』は、上記5つのすべての理論式に対応しています。
・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・(5)
表面自由エネルギー の成分を分散成分( )と水素結合と双極子・双極子相互作用に基づく成分( )に分けています。
ここで、固体の表面自由エネルギー は、 となり、液体の表面自由エネルギー は、 となります。
式(3)、(5)より
・・・・・・・・・・・・・・・・・・・・・・・(6)
が得られます。
固体の表面自由エネルギーにおける未知の2成分を求めるので、表面自由エネルギーが既知の2種類の液体を用います。
成分が既知の液体1の表面自由エネルギーを 、液体1と固体との接触角を とします。
成分が既知の液体2の表面自由エネルギーを 、液体2と固体との接触角を とします。
式(6)は液体1、液体2に関して次式のようになります。
・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・(8)
式(7)、(8)より、固体の表面自由エネルギーにおける未知の2成分 による2元1次方程式が導かれますので、これを解いて求めます。
基本的な考え方は、Owens and Wendtと同じですが、成分の考え方に若干の違いがあります。 Kaelbel and Uyの理論式では、表面自由エネルギーγの成分を分散成分( )と極性成分( )に分けています。 また、論文中では、計算に用いる2元1次方程式の行列式detを|D|として、解析結果の精度を判定しています。
Owens-Wendt-Rabel-Kaelble(OWRK)法とも呼ばれます。
|D|= ・・・・・・・・・・・・・・・・・・・・・・・(9)
|D|は分母となるため、|D|≠0でなければなりません。
また、Kaelbelは、0<|D|<1.0ならば表面自由エネルギーがとても大きな値になるとしており、|D|>10.0となる液体の組み合わせでナイロン6-6を元に検証を行っていますが、最終的には複数の液体の平均値を求めて、ナイロン6-6の成分を決定しています。
しかしながら、|D|の値がどうあれば良いかとは示されていませんでしたが、|D|の値が小さい場合は、誤差を大きく含んでいる可能性があるという指標になるでしょう。
・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・(11)
表面自由エネルギー の成分を分散成分( )と極性成分( )と水素結合成分( )に分けています。
ここで、固体の表面自由エネルギー は、 となり、液体の表面自由エネルギー は、 となります。
式(3)、(11)より
・・・・・・・・・・・・(12)
が得られます。
固体の表面自由エネルギーにおける未知の3成分を求めるので、表面自由エネルギーが既知の3種類の液体を用います。
成分が既知の液体1の表面自由エネルギーを とすると、 、液体1と固体との接触角を とします。
成分が既知の液体2の表面自由エネルギーを とすると、 、液体2と固体との接触角を とします。
成分が既知の液体3の表面自由エネルギーを とすると、 、液体3と固体との接触角を とします。
式(12)は液体1、液体2、液体3に関して次式のようになります。
・・・・・・・・(13)
・・・・・・・・(14)
・・・・・・・・(15)
式(13)、(14)(15)より、固体の表面自由エネルギーにおける未知の3成分 による3元1次方程式が導かれますので、これを解いて求めます。
Wuの論文では、主に高分子に対しての記述になっている点に留意した上で用いる必要があります。
・・・・・・・・・・・・・・・・・・・・・・・(16)
・・・・・・・・・・・・・・・・・・・・・・・(17)
表面自由エネルギー の成分を分散成分( )と極性成分( )に分けています。
ここで、固体の表面自由エネルギー は、 となり、液体の表面自由エネルギー は、 となります。
式(3)、(17)より
・・・・・・・・・・・・・・・・・・・・・・・(18)
が得られます。
固体の表面自由エネルギーにおける未知の2成分を求めるので、表面自由エネルギーが既知の2種類の液体を用います。
成分が既知の液体1の表面自由エネルギーを とすると、 となり 、液体1と固体との接触角を とします。
成分が既知の液体2の表面自由エネルギーを とすると、 となり 、液体2と固体との接触角を とします。
式(18)は、液体1、液体2に関して次式のようになります。
・・・・・・・・・・・・・・・・・・・・・・・(19)
・・・・・・・・・・・・・・・・・・・・・・・(20)
式(19)、(20)より、固体の表面自由エネルギーにおける未知の2成分 による2次方程式が導かれますので、これを解いて求めます。
酸・塩基理論では、LWとABの記号が用いられ、Lifshitz-van der Waals(LW)成分と、Lewis 酸・塩基(acid-base)成分とに分けられます。
酸・塩基成分は、更に電子受容成分(または酸性成分) と電子供与成分(または塩基成分) とに分けられます。
LW成分、酸・塩基成分の相互作用は、いずれも幾何平均で近似されます。酸・塩基成分を幾何平均で近似することの理論的根拠は乏しく、また、塩基成分が過大に評価される傾向があり、プローブ液体エネルギー値の設定についても、議論があります。
酸・塩基理論では、結局、固体の表面自由エネルギーにおける未知の3成分を求めることになりますので、表面自由エネルギーが既知の3種類の液体を用います。
・・・・・・・・・・・・・・・・・・・・・・・(21)
・・・・・・・・・・・・・・・・・・・・・・・(22)
・・・・・・・(23)
以下、Kitazaki and Hata(北崎・畑)理論と同様の方法で求めます。
理論の不完全性について
表面自由エネルギーに関する理論のおおもとはFowkesに行き着きます。Fowkesの論文を元に、OwensやWuなどがその理論を発展させて接触角から固体の表面自由エネルギーを求める考え方を提案しています。
しかし、Fowkesは、「固体の表面自由エネルギーには、融解(凝固)熱の寄与があり、この寄与を接触角からは求めることはできない」と述べていること、また、たくさんの専門家が関わり、複数の理論が乱立し確立された理論がないことからも、これで良いと言える理論式は現在存在していないことになります。
そうした中でも、何の手がかりもない中で評価をするよりは、仮定とする理論に準拠することで、方向性(優位性)が与えられることを期待して、一般的には表面自由エネルギーの計算が用いられています。液体の成分の比率や、考え方、方程式が異なることからも、用いる理論によって、結果が異なる事態に遭遇します。
こうした場合には、解析者自身で試行錯誤して最良の方法を選定していく必要があります。
接触角の値は何を代入すべきか
オプションの表面自由エネルギー計算ライセンスの場合、接触角の測定では時系列で取得するため、着液後何秒後の数値を用いればいいか迷うことがあります。
前提となるYoungの式では、液滴と固体のぬれ状態が平衡状態になった時に適用できますので、時系列で取得した接触角の変化がなくなった時点での値となります。
しかし現実には、一見平衡状態に達したように見えても、緩やかにぬれ拡がっていたり、あるいは蒸発の影響によって変化し続けている場合もあります。
このため、どの瞬間が平衡状態化を厳密に定義することができません。
そのため、グラフから概ね水平状態になった時間を求め、例えば1秒後の値を用いるなど解析者による基準をきめる必要があります。
また、接触角の測定結果にはばらつきが含まれますので、繰り返しによる平均値を用いることで、ばらつきの影響を排除する必要があります。よって、以下の指標を元にした接触角を入力することを推奨します。
- 複数回測定した平均値を用いる。
- 例えば着液後1秒後の数値を用いる、などの規定を設け接触角値を求める。
理論によって異なるプローブ液体の成分
前述のように、複数の理論があり確率されていないため、それぞれの理論ごとに同じプローブ液体でも成分が異なっています。
計算を行う理論と合わせることで理論に沿った解析結果になりますが、理論が確率していないため、別の理論の成分を用いて計算してはならないとは規定されていません。
プローブ液体は何を用いるべきか
プローブ液体の組み合わせを変えると、計算結果が変わり得ます。これは、表面自由エネルギーの理論自体が不完全であることに起因しますが、それ以外にもプローブ液体や接触角測定値にも誤差が含まれるためです。
そのため、複数の計算結果を比較する場合には、プローブ液体を限定するなどの工夫が必要になります。そうした中で、一般的に広く使われているのが、水・ジヨードメタン(ヨウ化メチレン)・n-ヘキサデカンとなります。
参照文献
- F.M.Fowkes,Ind.Eng.Chem.,Vol56,40(1964)
- D.K.Owens,and,R.C.Wendt,Journal of applied polymer science Vol.13,PP.1741-1747,(1969)
- D.H.Kaelble,J.Adhesion,Vol2(April 1970)
- 北崎,畑,日本接着学会誌,Vol.8,No.3,(1972)
- S.Wu,J.Polymer.Sci:Psrt C,No.34,PP.19-30(1971)
- J.Dispersion science and technology,11(1),75-81(1990)