表面張力の測定原理

表面張力、界面張力の測定方法には色々ありますが、代表的な手法をご紹介します。

ペンダント・ドロップ法（懸滴法）
プレート法（Wilhelmy法、懸垂法）
リング法（du Noüy法、輪環法、円環法）
最大泡圧法（泡の最大圧力法、バブルプレッシャー法）
毛管上昇法（Capillary-rise method）

ペンダント・ドロップ法（懸滴法）

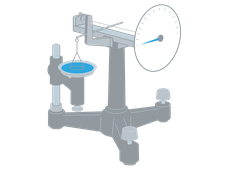
ペンダント・ドロップ法（Pendant drop method、懸滴法）は、垂直に設置した細管（注射針）先から液体を垂らし、落下しない程度の最大の懸滴（ドロップ）の形状より液体の表面張力を算出する方法です。細管先にできた懸滴は、液体量、密度差、表面・界面張力に依存するため、懸滴の形状解析により表面張力を算出することが可能です。

液体-気体間の表面張力だけでなく、液槽内で異なる液滴を吐出することにより液-液間の界面張力を測定することが可能です。

装置は、主に接触角計の液滴の吐出機構を利用して測定・解析を行います。

実際の測定は、シリンジの針先よりゲージを回しながら懸滴が落下しない最大限の懸滴を作ります。その後、表面張力計のCCDカメラが懸滴のサイズをリアルタイムに捉え、液体自体の表面張力を算出します。

解析方法としては、d/D法とカーブフィッティング法（Young－Laplace法）があります。

メリットとしては、

液滴サンプル量が少なくてすむ
高温環境や高圧環境などでも測定可能
表面張力・界面張力の経時変化を測定可能

などがあります。

一方デメリットとしては、

表面張力・界面張力の算出に密度値が必要
高粘度の液体の場合、シリンジからの吐出が困難

などがあります。

d/D法による測定原理

ds/de法とも呼ばれます。

測定原理は、懸滴の最大径Dを求め、懸滴の下端からDの長さ分上の径dとの関係から、液体の表面張力を求めることができます（図１）。

表面張力の関係式は、次式のとおりとなります。

γ = Δρg D^{2} \frac{1}{H}

$γ$ ：表面張力

$Δρ$ ：密度差

$ｇ$ ：重力加速度

1/H：d/Dによる補正係数

補正係数（1/H）は、d/Dの数値のレンジにより、下記表１より数値を代入して、以下の式から求められます。

\frac{1}{H} = \frac{B_{4}}{S^{a}} + B_{3} S^{3} - B_{2} S^{2} + B_{1} S - B_{0}

Sは、S=d/Dと定義します。

表１

Range of S a B₄ B₃ B₂ B₁ B₀

0.401-0.46 2.56651 0.32720 0 0.97553 0.84059 0.18069

0.46-0.59 2.59725 0.31968 0 0.46898 0.50059 0.13261

0.59-0.68 2.62435 0.31522 0 0.11714 0.15756 0.05285

0.68-0.90 2.64267 0.31345 0 0.09155 0.14701 0.05877

0.90-1.00 2.84636 0.30715 -0.69116 -1.08315 -0.18341 0.20970

0.401未満は、補正の必要がありません。

参考文献：Encyclopedia of Surface and Colloid Science volume 3

カーブフィッティング法（Young－Laplace法）による測定原理

懸滴の輪郭の形状（図２）は、Young－Laplace方程式とよばれる、次のような連立微分方程式で表すことができます。

\[ \begin{cases}\frac{dφ}{dS}=2+βZ-\frac{sinφ}{X}\\\\ \frac{dX}{dS}=cosφ\\\\ \frac{dZ}{dS}=sinφ\\\\ β=-\frac{ ∆pgb^{2}}{γ}\end{cases}\\\\ \]

b:懸滴最下部の主曲率半径。

S:懸滴輪郭の弧長。原点を基準に測る。ただし、ｂで規格化した値。

X:輪郭のX座標。ただし、ｂで規格化した値。

Z:輪郭のZ座標。ただし、ｂで規格化した値。

φ：Sにおける輪郭の接線の角度。

⊿ρ：懸滴相と周囲相との密度差。

g：重力加速度。

γ：界面張力。ただし、懸滴相、周囲相のいずれかが気体の場合は、表面張力。

β：形状因子。懸滴形状が球に近い場合は0に近くなります。

Young－Laplace方程式によって、懸滴を形成している液体の界面張力・密度差と輪郭の形状とが関連づけられています。

したがって、懸滴輪郭の形状を解析することにより（カーブフィッティングさせることにより）、液体の表面張力をより精密に求めることが可能です。

測定可能な機種：B100、B100W、A1000T

当社のペンダント・ドロップ法での算出方法について

懸滴の輪郭座標を取得します。
d/D法から得られた各種パラメータを初期値として、Young-Laplace 方程式から理論座標を算出します。
与えられた輪郭座標に対して非線形最小二乗法を適用して、Young-Laplace 方程式のパラメータを最適化・推定します。
推定されたパラメータから、界面張力を算出します。

プレート法（Wilhelmy法、懸垂法）

プレート法（Plate method、Vertical Plate method、Wilhelmy method、ウィルヘルミー法）とは、薄い白金プレート（もしくは薄いガラス板など。測定子とも呼ばれます。）をぶら下げておき、表面張力の測定対象の液体を入れた液槽を引き上げ接触した際に、プレートが液槽に引っ張られる力を測定する方法です。白金プレートと液体の接触角がゼロと仮定して表面張力を算出するため、白金プレートが完全に濡れている必要があります。実際には、一度白金プレートを浸漬させた後、再度引き上げるといった動作が必要になります。

γ = \frac{F}{L cos Θ}

$γ$ ：表面張力（mN/m）
F：測定力（白金プレートにはたらく力：mN）
L：白金プレートの周囲長さ（m）
θ：白金プレートと液体との接触角

デメリットとしては、

白金プレートが高価
測定の都度、白金プレートの洗浄が必要

等があります。

リング法（du Noüy法、輪環法、円環法）

リング法（du Noüy法、du Noüy method、ring method）とは、名前の通りリングを用いて表面張力を測定する手法です。

リング法の原理は、リングを液体に浸したあと、徐々に引き上げていき、リングと液面の間にできた膜が切れる瞬間にかかる力（液体がリングを引っ張る力）を測定する方法です。リングに作用する下方向に発生する力は、リングの表裏に膜が発生するため、円周と表面張力を掛け合わした数値の2倍になり、下記の式（１）が成り立ちます。リングの材質は、白金（Pt）で作られるものが主流です。

$FC = 2 π R ・ 2 ・ γ$ ・・・（1）

すなわち、

γ = \frac{F}{4 π R} C

$γ$ ：表面張力（mN/m）
F：引き上げる力
R：リングの半径
C：補正項

最大泡圧法（泡の最大圧力法、バブルプレッシャー法）

最大泡圧法（泡の最大圧力法、バブルプレッシャー法、Maximun Bubble Pressure Method）とは、液体中のプローブに気体を送り、プローブ先端より気泡が発生した時の最大圧力を測定して表面張力を測定する方法です。

毛管上昇法（Capillary-rise method）

細管の内壁と液体のなじみやすさが、「ぬれ」に依存する毛管現象（毛細管現象、capillary action）を利用して、液体の表面張力を測定する方法です。

図1のように細管内壁で液面が上昇している状態では、「細間内壁で表面張力により液面が上昇している力」と「液体に働く重力」は釣り合っています。その為、下記式が成り立ち、液面の上昇距離(h)や接触角(θ)を測定し、表面張力を求めることが可能です。

「細間内壁で表面張力により液面が上昇している力」=「液体に働く重力」

2 π r γ cosθ = π r^{2} hρg

すなわち

γ = \frac{π r^{2} hρg}{2 π r cosθ}

が成り立ちます。

$γ$ ：表面張力（mN/m）
θ：内壁の接触角
r：細管の内半径
ρ：液体の密度
g：重力加速度

表面張力の測定事例はこちら

Range of S	a	B₄	B₃	B₂	B₁	B₀
0.401-0.46	2.56651	0.32720	0	0.97553	0.84059	0.18069
0.46-0.59	2.59725	0.31968	0	0.46898	0.50059	0.13261
0.59-0.68	2.62435	0.31522	0	0.11714	0.15756	0.05285
0.68-0.90	2.64267	0.31345	0	0.09155	0.14701	0.05877
0.90-1.00	2.84636	0.30715	-0.69116	-1.08315	-0.18341	0.20970