測定原理（粉体濡れ性評価）

粉体の濡れ性評価について

一般的に濡れ性測定とは、固体表面に液体を付着させ、その親和性を計測するために、接触角計が用いられます。これは、固体表面の濡れ性を評価する手法としては非常に有用ですが、粉体の濡れ性を測定するには一般的ではありません。なぜかと言いますと、固体表面に対象の粉体を敷き詰めて、液体を付着させた場合、撥水性の粉体であれば接触角は測定できます。

粉体の接触角

しかし親水性の粉体の場合、固体表面の濡れ広がりと違い、浸透してしまいます。経過時間毎の濡れ広がり（接触角）かつ浸透していく様とパラメーターが2つになり定量的な測定が困難にもなります。また粉体の敷き詰め方によっても表面状態が大きく変化してしまうため、再現性も低くなります。そこで、粉体の濡れ性を測定する際は、「浸透する」という点に着目し、その「浸透速度」で測定するという手法を取ります。つまり、粉体の濡れ性測定では、「接触角」ではなく、「浸透速度法（ウォッシュバーン法）」を用いて、経過時間毎の浸透力（濡れ上がり）を測定していきます。

下記に、浸透速度法について詳しく説明していきます。

粉体濡れ性評価受託についてはこちら

浸透速度法（Lucas-Washburnの式）とは

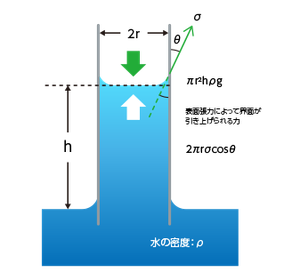
浸透速度法とは、粉体を液体に浸し、毛管現象によって液体が粉体内に浸透し濡れ上がる度合いを測定する方法です。浸透速度法は以下の式、ルーカス-ウォッシュバーン（Lucas-Washburn）の式から求めることが知られています。

\frac{h^{2}}{t} = \frac{rσcosθ}{2η}

h	：	液体の浸透高さ
r	：	粉体を充填するカラムの半径
σ	：	液体の表面張力
θ	：	接触角
η	：	液体の粘度
t	：	時間

実測方法とLucas-Washburn式の導出

実際の測定では、カラムと呼ばれる筒状の容器に粉体を充填し、それを液体に浸します。粉体と液体の濡れ性が良好であれば、液体は粉体層内を濡れ上がります。

粉体接触角　カラム写真

この時、図1のように液高さhでの液体に働く重力と表面張力の釣り合いより毛管上昇高さhが求められます。

$π r^{2} hρg = 2 πrσcosθ$ ・・・・（１）

ρ：液体の密度

粉体接触角測定　ルーカス-ウォッシュバーン（Lucas-Washburn）の式図1 — 図１

左辺は上昇した水位の質量 $π r^{2} hρ$ [kg]に重力 $g[m/ s^{2}$ ]を乗じたもの、右辺は単位長さあたりの表面張力 σ[N/m]がガラス管カラム1周分 $2πr$ [m]に掛かっている事を表しています。

粉体接触角測定　ルーカス-ウォッシュバーン（Lucas-Washburn）の式図2 — 図2

$h = \frac{2σcosθ}{rρg}$ ・・・・（２）

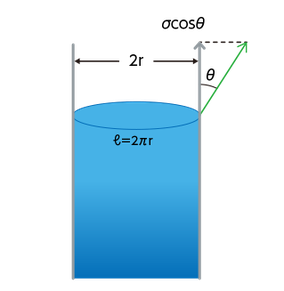
この値が高いほど管壁に対する液体の親和性が高いことを意味します。粉体の場合、カラムの底面をメッシュフィルタなどで覆い、粉体を充填したものを液体に浸します。

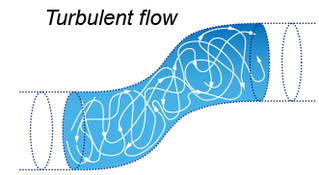
その時、液体は表面張力によって吸い上げられ、圧力損失Δp[Pa]を生じます。また、吸い上げられる粉体内の流れを層流※と仮定すると、ハーゲン・ポアズイユの法則（Hagen-Poiseuille’s law）で表すことが出来ます。

※層流とは、流体が規則正しく運動している流れのこと。乱流の反対の意。

層流イラスト

乱流イラスト

円管内を流れる流量Qは次のような式（３）で表されます。

$Q = \frac{π r^{4} ΔP}{8 ηh}$ 　・・・（３）ポアズイユ式

圧力損失ΔPは下記の通り表すことができます。

$ΔP = hρg$ ・・・・（４）

先ほどの毛管上昇のつり合いの式（１）に代入すると、

$π r^{2} hρg = 2 πrσcosθ$ ・・・・（１）

$π r^{2} ΔP = 2 πrσcosθ$ ・・・（５）

上記のポアズイユの式を変形し、

$ΔP = \frac{8ηhQ}{π r^{4}}$ 　・・・（６）

(６)式を(５)に代入すると、

π r^{2} ・ \frac{8ηhQ}{π r^{4}} = 2 πrσcosθ

h = \frac{π r^{3} σcosσ}{4ηQ}

$h = \frac{rσcosθ}{4η (\frac{Q}{π r^{2}})}$ ・・・・（７）

流速V(m/s)=流量Q(m³/s)÷断面積S(m²)で表されることから、

V = \frac{Q}{π r^{2}}

流速（V）は、時間の微小変化分（dt）に対する、濡れ上がり距離の変化分（dh）に等しいので、

V = \frac{dh}{dt}

\frac{Q}{π r^{2}} = \frac{dh}{dt}

式（７）に代入し、

h = \frac{rσcosθ}{4η (dh/dt)}

h･dh = \frac{rσcosθ}{4η} dt

\int h･dh = \int \frac{rσcosθ}{4η} dt

\frac{1}{2} h^{2} = \frac{rσcosθ}{4η} t

h^{2} = \frac{rσcosθ}{2η} t

$\frac{h^{2}}{t} = \frac{rσcosθ}{2η}$ 　・・・（８）

実際の装置での測定

実際の装置では液体の浸透高さｈを測定する代わりに、浸透重量Ｗの変化を測定する仕様になっています。

液体の浸透高さｈと浸透重量Wの関係は、式（９）のようにあらわせます。

$h = \frac{W}{Sερ}$ 　・・・（９）

h	：	液体の浸透高さ
W	：	浸透重量
ρ	：	液体の密度
ε	：	粉体の空隙率（くうげきりつ）
S	：	粉体の断面積

(９)式を(８)に代入すると、浸透重量Wの2乗と浸透時間tの関係式を導くことができます。

\frac{W^{2}}{t} = {(Sερ)}^{2} \frac{rσcosθ}{2η}

Washburnの式より、浸透重量Wの2乗と浸透時間tは直線関係にあるため、その傾きを求めることで浸透速度を比較することができます。